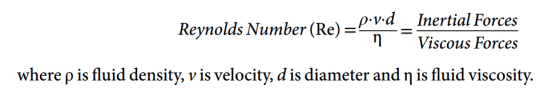Category Archives: Physics for anesthesiologist

Latent Heat and its applications in anesthesia practice

Posted on by
  • Heat capacity: The heat energy required to raise the temperature of a given object by one degree. (J.K−1 or J.°C−1)
  • Specific heat capacity: The heat energy required to raise the temperature of one kilogram of a substance by one degree. (J.kg−1.K−1 or J.kg−1.°C−1)
  • But not all heat energy results in a temperature change.
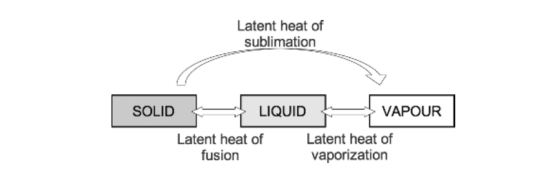
  • Latent heat: This is the heat energy that is required for a material to undergo a change of phase. (J) The heat is not utilised for raising the temperature, but for changing the phase.
  • If heat is applied to matter, temperature increases until the melting or boiling point is reached. At these points the addition of further heat energy is used to change the state of matter from solid to liquid and from liquid to gas. This does not cause a change in temperature. The energy required at these points is referred to as latent heat of fusion and latent heat of vaporisation, respectively.
  • Specific latent heat is the heat required to convert one kilogram of a substance from one phase to another at a given temperature.
  • Screen Shot 2018-07-11 at 5.43.58 PM
  • As temperature increases, the amount of additional energy required to overcome the intermolecular forces of attraction falls until the critical temperature of a substance is reached. At this point the specific latent heat is zero, as no further energy is required to complete the change in state of the substance.

APPLICATIONS

  • Variable bypass vaporisers function by passing a small amount of fresh gas through the vaporising chamber, which is fully saturated with anaesthetic vapour. This removes vapour from the chamber. Further vaporisation from the anaesthetic liquid must occur to replace the vapour removed, which requires energy from the latent heat of vaporisation. This cools the remaining liquid, reducing the saturated vapour pressure and thus the concentration of anaesthetic vapour delivered, resulting in an unreliable device.
  • Temperature compensation features help to overcome this problem; a copper heat sink placed around the vaporising chamber is one such example. Copper has a high heat capacity and donates energy required for latent heat of vaporisation, maintaining a stable temperature and reliable delivery of anaesthetic agent.
  • Evaporation of sweat is another example. It requires the latent heat of vaporisation, which is provided by the skin’s surface, exerting a cooling effect upon the body.
  • Evaporation from open body cavities can be a cause of significant heat loss from patients while under anaesthesia.
  • These principles are also applicable to blood transfusion. Blood is stored at 5°C and has a specific heat capacity of 3.5 kJ·kg−1·K−1. If cold blood were transfused into a patient without pre-warming, the heat energy required to warm the blood to body temperature would need to be supplied by the patient, which would have a significant cooling effect.

Ohm’s Law

Posted on by
  • The strength of an electric current varies directly with the electromotive force (voltage) and inversely with the resistance. So I = V/R or V = IR where V is voltage, I is current and R is resistance.
  • The equation can be used to calculate any of the above values when the other two are known. When R is calculated, it may represent resistance or impedance depending on the type of circuit being used (AC/DC)
  • Resistance: The opposition to flow of direct current. (ohms, Ω)
  • Reactance: The opposition to flow of alternating current. (ohms, Ω)
  • Impedance: The total of the resistive and reactive components of opposition to electrical flow. (ohms, Ω)
  • The reactance of an inductor is high and comes specifically from the back electromotive force that is generated within the coil. It is, therefore, difficult for AC to pass.
  • The reactance of a capacitor is relatively low but its resistance can be high; therefore, direct current (DC) does not pass easily.

Thermistors and their use in anesthesia

Posted on by
  • A thermistor is a temperature-sensitive resistor whose resistance changes with temperature.
  • Most temperature-sensitive resistors are constructed from a semiconductor material (carefully chosen metal oxides) and the resistance increases with a fall in temperature (they have a negative temperature coefficient)
  • So they are known as negative thermal conductivity (NTC) thermistors.
  • A Wheatstone bridge circuit is used to measure the resistance accurately.
  • The main disadvantage of thermistors is the non-linear resistance versus temperature characteristic, although this can be compensated for using an appropriate calibration equation programmed into an electronic measurement system.
  • Thermistors remain highly popular due to their cost, miniature size and convenience.
  • Thermistor probes are commonly placed in the nasopharynx, oesophagus, rectum or bladder (integrated with a urinary catheter).
  • They have excellent accuracy and their small mass means that there is a quick response to variations in temperature.
  • But they ‘age’ and their resistance changes with time. They also exhibit hysteresis.
  • True or False? ‘A thermistor comprises a junction of dissimilar metals’
  • Answer: False. Dissimilar junctional metals are thermocouples
  • True or false: ‘A thermistor demonstrates the Seebeck effect’
    Answer: False. The Seebeck effect applies to themocouple

Turbulent flow and it’s clinical applications

Posted on by

 

  • The flow pattern of a river running over rapids is very different to the steadily flowing river (laminar flow). Here, the water’s path of travel becomes far less predictable than for laminar flow. This is an example of turbulent flow. An intermediate example is water flowing near the bank of a steadily flowing river, which often tends to meander, turning round in gentle circles. This is an example of eddies, the forerunner to full-blown turbulence.
  • As flow is, by definition, unpredictable, there is no single equation that defines
    the rate of turbulent flow as there is with laminar flow.
  • But, in well controlled circumstances the point at which flow changes from laminar to turbulent flow can be estimated using the Reynolds number, Re, which is named after Osborne Reynolds (1842–1912) of Manchester University, an engineering professor.
  • The Reynolds number allows us to predict whether turbulent or laminar flow would occur in a given system. The Reynolds number is a dimensionless quantity, i.e. it has no units. It is defined as the ratio of inertial and viscous forces. A Reynolds number <2000, where viscous forces predominate, predicts flow to be laminar. Between 2000 and 4000, both laminar and turbulent flow are anticipated. Above 4000, flow is likely to be completely turbulent because inertial forces are dominant. Critical flow is the point above which turbulent flow commences, which occurs at a Reynolds number of around 2000.
  • reynolds
  • Viscosity is the important property for laminar flow
  • Density is the important property for turbulent flow
  • Reynold’s number of 2000 delineates laminar from turbulent flow (Tim and Pinnock: Re < 1000 is associated with laminar flow, while Re > 2000
    results in turbulent flow)
  • A high Reynolds number means that the inertial forces dominate, and any eddies in the flow will be easily created and persist for a long time, creating turbulence
  • In a given airway with a known gas and flow velocity, the likelihood of turbulent flow can be predicted from Re.
  • But the pressure–flow relationship for turbulent flow is different because the pressure gradient producing the flow is:
  • >Proportional to (flow velocity)2
    >Dependent on gas density and
  • >independent of viscosity
    >Inversely dependent on (radius)5
  • APPLICATIONS:
  • Both laminar and turbulent flow exist within the respiratory tract, usually in mixed patterns. Turbulence increase the effective resistance of an airway compared with laminar flow. Turbulent flow occurs at the laryngeal opening, the trachea and the large bronchi (generations 1–5) during most of the respiratory cycle. It is usually audible and almost invariably present when high resistance to gas flow is encountered
  • The principal sites of resistance to gas flow in the respiratory system are the nose and the major bronchi rather than the small airways. Since the cross-sectional area of the airway increases exponentially as branching occurs, the velocity of the airflow decreases markedly with progression through the airway generations, and laminar flow becomes predominant below the fifth generation of airway

Laminar flow (For clinical applications, see post: Turbulent flow)

Posted on by
  • Screen Shot 2018-07-03 at 9.22.44 AM
  • When watching a steadily flowing river, the flow of water may be seen to be fastest in the middle, while near the banks of the river the water flows more slowly. This behaviour is also observed in fluid travelling slowly along a wide straight cylindrical tube, where the fastest velocity occurring in the centre of the tube and the slowest at the edge where there is friction between the wall of the tube and the fluid. This is known as laminar flow.
  • Viewed from the side as it is passing through a tube, the leading edge of a column of fluid undergoing laminar flow appears parabolic. The fluid flowing in the centre of this column moves at twice the average speed of the fluid column as a whole. The fluid flowing near the edge of the tube approaches zero velocity.
  • Hagen (in 1839) and Poiseuille, a surgeon (in 1840) discovered the laws governing laminar flow through a tube. If a pressure P is applied across the ends of a tube of length, l, and radius, r. Then the flow rate, Q, produced is proportional to:
    *The pressure gradient (P/l)  *The fourth power of the tube radius  *The reciprocal of fluid viscosity . This is often combined as:
  • Screen Shot 2018-07-09 at 11.31.14 AM
  • where Q is flow, ΔP is pressure gradient, r is radius, η is fluid viscosity and l is length
  • Also Q = Pressure Difference/ Resistance; so Resistance= Pressure Difference / Q. When we apply H-P equation into this: Resistance, is dependent on the length of the tube and the viscosity of the fluid, but inversely related to the fourth power of the radius.
  • Also note: Viscosity is the important property for laminar flow, whereas density is the important property for turbulent flow. Reynold’s number of 2000 delineates laminar from turbulent flow

VIVA SCENE: DIATHERMY AND THE ANESTHESIOLOGIST

Posted on by
  • WHY WE SHOULD KNOW? 1.Anesthesiologist may be blamed if burns occurs due to malposition of the plate 2. It can interfere with monitors e.g. ECG and pulseoximeters 3. It can disrupt pacemaker function in a patient, having it.
  • Diathermy depends on the heat generated when a current pass through a tissue and is used to coagulate blood vessels and cut through tissues
  • A high frequency current is necessary for this, as myocardium is sensitive to DC and low frequency AC [the usual mains frequency of 50 Hz] will precipitate VF. Very high frequencies have minimal tissue penetration and pass without harming the myocardium
  • A 0.5 MHz alternating sinewave is used for cutting and a 1.0-1.5 MHz pulsed/ damped sinewave pattern is used for coagulation
  • UNIPOLAR DIATHERMY & PROBLEMS: Here the forceps represent one electrode (small area, high current density and significant heat generation) and the diathermy plate ( indifferent electrode) over the patient represent the other electrode (large area, less heat). If the the plate is malpositioned, the current may pass through any point of metal contact *like ECG electrodes, metal poles of lithotomy, operation table etc, and may result in passage of high current density as the area of contact is small, resulting in a burn. So we should ensure that the plate is in close and proper contact with a large, highly perfused (will dissipate heat) area of skin (adhesive gels are useful). If we place it near to metal prosthesis (e.g. Hip), which has a low resistance than tissue, it will generate a high current density, resulting in burns. A unipolar diathermy can generate 150-400 Watts of energy.
  • BIPOLAR DIATHERMY: Current passes between the two blades of the forceps; so requires no plate; safer in patients with pacemaker. But can generate only 40 Watts of energy. So efficacy is less and may be used for coagulation of small blood vessels
  • OTHER PROBLEMS: Sometimes diathermies may cause ignition of skin preparation spirit. Newer diathermies dont have earthing; but if your machine is having earthing, an inappropriate earthing will result in current passing through other routes mentioned above*, resulting in burns.
  • Cautious use of diathermy is required in patients with pacemakers:
    Screen Shot 2018-06-28 at 12.54.13 PM

NITROUS OXIDE ISOTHERM

Posted on by

  • An isotherm is a line of constant temperature

  • Compressed gases in a cylinder can either stay as a gas, or change state to form a liquid due to the higher pressure (both carbon dioxide and nitrous oxide do this).

  • A graph of pressure against time for nitrous oxide is shown below. The isothermal lines are shown for 40°C, 36.6°C and 20°C.

  • At 40°C, nitrous oxide is above its critical temperature and so it is a gas no matter whatever pressure is being applied.

  • When it is compressed (moving from right to left along the isotherm) the pressure increases smoothly. At 36.6°C (the critical temperature), as soon as the pressure reaches the critical pressure (72 bar), the gas becomes a liquid.

  • At 20°C, once the pressure reaches 52 bar (the saturated vapour pressure of nitrous oxide at 20°C), some of the gas condenses so that liquid and vapour are both present. Further decreases in volume cause more vapour to condense, with no associated rise in pressure. When all the vapour has condensed to a liquid, any further reduction in volume causes a rapid rise in pressure.

  • In most circumstances, nitrous oxide is stored below its critical temperature of 36.4 C. It therefore exists in the cylinder as a vapour in equilibrium with the liquid below it.

  • To determine how much nitrous oxide remains in a given cylinder, it must be weighed, and the weight of the empty cylinder, known as the tare weight, subtracted. Using Avogadro’ s law, the number of moles of nitrous oxide may now be calculated. V/n= K, where V = volume of gas, n = amount of substance of the gas, K = a proportionality constant

  • Using the universal gas equation, the remaining volume can be calculated. PV = nRT, where P = pressure, V = volume, n = the number of moles of the gas, R = the universal gas constant (8.31 J/K/mol), T = temperature

GAS LAWS

Posted on by
  • Boyle’s law
  • At a constant temperature, the volume of a fixed amount of a perfect gas varies inversely with its pressure.
  • PV = K or V ∝ 1/P . Also P 1 V 1 = P 2 V 2
  • Ⓜ️NEMO> water Boyle’s at a constant temperature
  • Example: P 1 V 1 relates to the pressure and volume in the cylinder and P 2 V 2 relates to the pressure and volume at atmospheric pressure. For example, oxygen is stored at 13 800 kPa (absolute pressure) in gas cylinders. If the internal volume of the cylinder is 10 litres, the volume this cylinder will provide at atmospheric pressure: 13 800 × 10 = 100 × V 2. So V 2 = 1380 litres. However, 10 litres will remain within the cylinder, so 1370 litres will be usable at atmospheric pressure.
  • Charles’ law
  • At a constant pressure, the volume of a fixed amount of a perfect gas varies in proportion to its absolute temperature.
  • V/T = K or V ∝ T
  • Ⓜ️NEMO> Prince Charles is under constant pressure to be king
  • Gay–Lussac’s law (The third gas law)
  • At a constant volume, the pressure of a fixed amount of a perfect gas varies in proportion to its absolute temperature.
  • P/T = K or
  • P∝T
  • Perfect gas: A gas that completely obeys all three gas laws or A gas that contains molecules of infinitely small size, which, therefore, occupy no volume themselves, and which have no force of attraction between them.
  • It is important to realize that this is a theoretical concept and no such gas actually exists. Hydrogen comes the closest to being a perfect gas as it has the lowest molecular weight. In practice, most commonly used anaesthetic gases obey the gas laws reasonably well.
  • Other gas laws of relevance:
  • Avogadro’s hypothesis: at a constant temperature and pressure, all gases of the same volume contain an equal number of molecules.
  • Dalton’s law: the pressure exerted by a mixture of gases is the sum of the partial pressures of its constituents.
  • Henry’s law: at a constant temperature, the amount of gas dissolved in a given volume of liquid is directly proportional to the partial pressure of that gas in equilibrium with the liquid.
  • Henry’s law can be used to show that the amount of oxygen dissolved in blood is proportional to the partial pressure of oxygen in the alveolus. The amount of dissolved oxygen carried in blood is 0.023 ml·dl −1 ·kPa −1 . At atmospheric pressure, this accounts for a very small and insignificant fraction of oxygen delivery. However, under hyperbaric conditions, the dissolved fraction increases and becomes a more significant source of oxygen delivery to tissues
  • At absolute zero, the theoretical volume of an ideal gas is zero. Real gases have liquefied before this point.
  • Boyle’s, Charles’ and Gay-Lussac’s law are combined to form the ideal gas law.

Damping

Posted on by
  • Damping describes the resistance of a system to oscillation resulting from a change in the input. Damping is the result of frictional forces working in that system. So following a change in input there are several possible outcomes for the system:
  • Perfect Response: any change in input would be instantly and accurately reflected in the output
  • Under-damped – the output changes quickly in response to the step up in input, but it overshoots and then oscillates around the true value, before coming to rest at it. It will take some time before the true value is displayed and the peaks and troughs will over and underrepresent the true value. In a dynamic system, e.g. intra-arterial BP, the constantly changing input may result in wild fluctuations, rendering an under-damped system very inaccurate (although the MAP is still correct).
  • Critically damped – the response and rise time of the system are longer than an under-damped response, but there is no significant overshoot and oscillations are minimal. ‘D’ is the damping factor and, by convention, in a critically damped system D = 1.
  • Over-damped – defined as damping greater than critical. The output here could potentially change so slowly that it never reaches the true value. In a dynamic system, the response time may be too slow for the system to be useful.
  • Optimally damped – in reality in clinical measurement systems, critical damping is not ideal and we are prepared to accept a few oscillations and some overshoot to achieve a faster response time. Hence, our systems are ‘optimally damped’ where 64% of the energy is removed from the system and D = 0.64. There is a 7% overshoot in this case.
  • N.B: The ‘response time’ is the time taken for the output to reach 90% of its final reading. The ‘rise time’ is the time taken for the output to rise from 10 to 90% of its final reading.
  • All instruments will possess damping that affects their dynamic response. This includes mechanical, hydraulic, pneumatic and electrical devices. In an electromechanical device such as a galvanometer there are mechanical moving parts such as the meter needle and bearings. Damping in these components arises from frictional effects on their movement. This may arise unintentionally or may be applied as part of the instrument design to control oscillation of the needle when it records a measurement. In a fluid (gas or liquid) operated device, damping occurs due to viscous forces that oppose the motion of the fluid. In an electrical system, damping is provided electronically by electrical resistance that opposes the passage of electrical currents.
  • Damping is an important factor in the design of any system. In a measurement system it can lead to inaccuracy of the readings or display:
  • Under-damping can result in oscillation and overestimation of the measurement.
  • Over-damping can result in underestimation of the measurement.
  • Critical damping is usually an optimum compromise resulting in the fastest steady-state reading for a particular system, with no overshoot or oscillation.

Pressure and it’s measurement by manometer

Posted on by